Terület kiszámítása

Ez az oldal azokat az alapvető tudnivalókat tartalmazza, amelyeket tudnod kell ahhoz, hogy megértsd és kiszámítsd a leggyakoribb alakzatok, például négyzetek és téglalapok, háromszögek és körök területét.

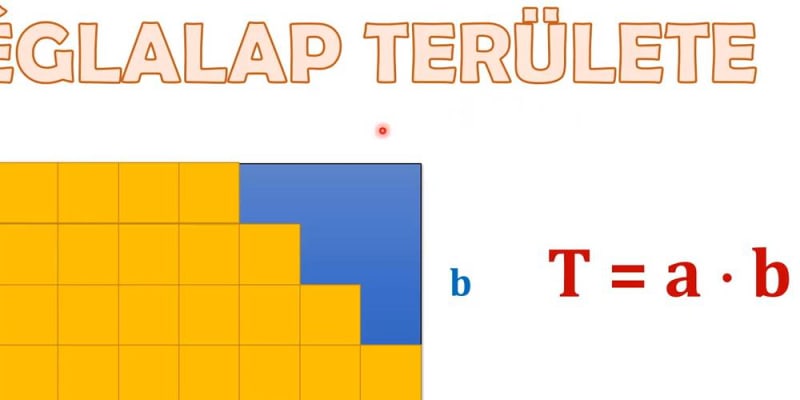
Területszámítás a rácsos módszerrel

Ha egy alakzatot egy méretarányos rácsra rajzolunk, akkor a területet az alakzaton belüli rácsnégyzetek számának megszámlálásával határozhatjuk meg.

Számozott rács, amely segít kiszámítani egy alakzat területét. Ebben a példában 10 rácsnégyzet van a téglalap belsejében. Ahhoz, hogy a rácshálós módszerrel meg tudjuk találni a terület értékét, tudnunk kell, hogy egy rácsnégyzet mekkora méretet képvisel.

Ebben a példában centimétert használunk, de ugyanez a módszer bármely hossz- vagy távolságegységre alkalmazható. Használhatunk például hüvelyk, méter, mérföld, láb stb. mértékegységeket. Egy rácsháló használata egy alakzat területének kiszámításához.

Ebben a példában minden egyes rácsnégyzet szélessége 1 cm, magassága pedig 1 cm. Más szóval minden egyes rácsnégyzet egy "négyzetcentiméter".

Számold meg a rácsnégyzeteket a nagy négyzet belsejében, hogy megtudd a területét. 16 kis négyzet van, így a nagy négyzet területe 16 négyzetcentiméter.

A matematikában a "négyzetcentimétert" cm2-re rövidítjük. A 2 azt jelenti, hogy 'négyzetcentiméter'.

Minden négyzetrács 1 cm2.

A nagy négyzet területe 16 cm2.

A négyzetek megszámlálása egy rácson a terület kiszámításához minden alakzat esetében működik - feltéve, hogy a rácsméretek ismertek. Ez a módszer azonban nagyobb kihívást jelent, ha az alakzatok nem illeszkednek pontosan a rácsra, vagy ha a rács négyzeteinek törtrészeit kell megszámolnunk.

1 cm-es négyzetrács egy alakzat területének kiszámításához.

Ebben a példában a négyzet nem pontosan illeszkedik a rácsra.

A területet mégis ki tudjuk számolni a rácsnégyzetek megszámolásával.

A rácson 25 teljes négyzet van

10 fél négyzet - 10 fél négyzet ugyanannyi, mint 5 teljes négyzet.

Van még 1 negyed négyzet - (egy egész négyzet ¼-e vagy 0,25-e).

Add össze az egész négyzeteket és a törteket: 25 + 5 + 0,25 = 30,25.

A négyzet területe tehát 30,25 cm2 .

Ezt 30¼cm2 -ként is leírhatod.

Bár a rács használata és a négyzetek számolása egy alakzaton belül nagyon egyszerű módja a terület fogalmának elsajátításának, kevésbé hasznos a pontos terület meghatározásához összetettebb alakzatok esetében, amikor a rács négyzeteinek sok tört része adható össze.

A területet egyszerű képletekkel is ki lehet számítani, attól függően, hogy milyen típusú alakzattal dolgozol.

Egy másik gyakori probléma a határ

- egy másik alakzaton belüli alakzat - területének meghatározása. Ez a példa egy mezőt körülvevő utat mutat - az út 2 m széles. Ebben a példában is többféleképpen lehet kiszámítani az ösvény területét.

Tekinthetjük az ösvényt négy különálló téglalapnak, kiszámíthatjuk a méreteiket, majd a területüket, végül pedig összeadhatjuk a területeket, hogy megkapjuk a végeredményt. Gyorsabb megoldás az egész alakzat területének és a belső téglalap területének kiszámítása. Az egészből kivonjuk a belső téglalap területét, így megkapjuk az útvonal területét.

Ábra, amely bemutatja, hogyan kell kiszámítani egy alakzat határának területét.

Az egész alakzat területe 16 m × 10 m = 160 m2.

A középső rész méreteit ki tudjuk számítani, mert tudjuk, hogy a szélén lévő út 2 m széles.

Az egész alakzat szélessége 16m, az egész alakzaton átvezető út szélessége pedig 4m (2m az alakzat bal oldalán és 2m a jobb oldalán). 16m - 4m = 12m

Ugyanezt a magassággal is megtehetjük: 10m - 2m - 2m - 2m = 6m.

Tehát kiszámítottuk, hogy a középső téglalap 12m × 6m.

A középső téglalap területe tehát: 12m × 6m = 72m2.

Végül a középső téglalap területét levonjuk az egész alakzat területéből. 160 - 72 = 88m2.

Az ösvény területe 88m2.

Körök területei

Egy kör területének kiszámításához ismerned kell az átmérőjét vagy sugarát.

A kör átmérője és sugara

Egy kör átmérője a kör egyik oldalától a másikig tartó egyenes hossza, amely a kör középpontján halad át. Az átmérő a sugár hosszának kétszerese (átmérő = sugár × 2).

A kör sugara a kör középpontjától a kör széléig tartó egyenes hossza. A sugár az átmérő fele. (sugár = átmérő ÷ 2)

Az átmérőt vagy a sugarat a kör bármely pontján megmérheted - a lényeg, hogy olyan egyenessel mérj, amely a kör középpontján halad át (átmérő) vagy a kör középpontján végződik (sugár).

A gyakorlatban a körök mérésekor gyakran egyszerűbb az átmérőt megmérni, majd osztani 2-vel a sugár megadásához.

A sugárra a kör területének kiszámításához van szükséged, a képlet a következő:

A kör területe = πR2.

Ez azt jelenti, hogy:

π = Pi egy állandó, amely 3,142-nek felel meg.

R = a kör sugara.

R2 (sugár négyzete) azt jelenti, hogy sugár × sugár.

Ezért egy 5 cm sugarú kör területe:

3,142 × 5 × 5 = 78,55 cm2 .

Egy 3 m átmérőjű kör területe:

Először is kiszámítjuk a sugarat (3m ÷ 2 = 1,5m).

Ezután alkalmazzuk a képletet:

πR2

3.142 × 1.5 × 1.5 = 7.0695.

A 3m átmérőjű kör területe 7,0695m2.